19世紀末から20世紀初頭にかけて、シカゴから始まった建築の高層化競争をニューヨークが引き継ぎ、1930年には、高さ300メートルの<クライスラービル>

が実現するに及んで、ようやく30年以上前に完成したパリのエッフェル塔の高さを超えることになります。その翌年に、102階、高さ378メートルの<エンパイアステート・ビル>

が完成するまで、猛烈な勢いで超高層ビルが建設され、マンハッタンのスカイラインは新しいビルが建てられる度に、めまぐるしく変化していきました。1900年からの30年間で、8回も世界一位の座が更新されることになります。
この当時のビルは組積による「ベアリングウォール構造」で、鉄骨造のフレーム内をレンガや石の壁で塗り固めたものでした。ベアリングウォール構造により、鉄骨のラーメンフレームに比べて、建物の剛性は数倍に高まりましたが、組積造の壁はあまりにも重く、その施工には手間と時間がかかりすぎました。このような非合理で不経済な工法は、長続きしませんでした。
アメリカ東海岸の超高層では、荷重に対する考え方が、日本と大きく異なりました。アメリカの超高層ビルでもっとも支配的な外力は風荷重であり、これによって建物に有害な変形や振動が生じないように剛性を高めることになります。対して日本では、風荷重だけでなく、地震に対する配慮が必要になります。剛性をむやみに高めることは、地震入力の増大につながり、構造検討上、不利側に働く恐れがあります。日本では、地震と風を同時に見据えながら、堅すぎず、柔らかすぎない、ほどよい剛性バランスを探りださなくてはいけません。アメリカ東海岸では、風荷重のみを考えればよいので、その設計手法は、とにかくガチガチに剛性を高める工夫が特徴的です。
世界を見渡して、摩天楼の名に最もふさわしいとも言えるのが「ニューヨーク」。200メートルを超える超高層ビルが40棟近くあるのは、世界でもニューヨークだけです。米経済誌フォーブスの「摩天楼都市番付」でも毎年世界1位に輝いています。アメリカという国を代表するパワフルなアイコンとして、西海岸のハリウッド、ラスベガスと並んで、東海岸ではニューヨーク高層ビル群が、そのイメージ喚起力で抜きん出ているのではないでしょうか。今回から、ニューヨークの高層ビル群について、建築構造に焦点を当てて、その建設技術の変遷、歴史、また高層ビル建設のイノベーションに貢献した人物等について、ご紹介していきます。
アメリカにおける建築の花形は、何といっても超高層ビルであり、その歴史はそのままアメリカにおける建築構造の発展史に重なります。アメリカにおける高層化の流れは、実は、ニューヨークではなく、シカゴから始まりました。ジョン・ウェルボーン・ルートやルイス・サリバンらを代表とする「第一シカゴ派」と呼ばれる人々が活躍し、骨組みに鉄骨造を用い、外観をレンガで装飾したビルを次々と建設しました。それらのビルは最高でも16階建て程度でしたが、当時の人々からすればそれでも十分に高くそびえ立った建物であり、「スカイスクレパー」(空を削るもの)と呼ばれました。
しかし、これら「第一シカゴ派」の仕事は鉄骨造が組積造よりも高層の建物を建設可能であることを世に示しましたが、技術の発展を促すほどのインパクトは持ち得ず、鉄という材料が持つポテンシャルからすれば、その高さはあまりに低く、その限界を引き出すまでに至りませんでした。
この後に、高層ビル建設でシカゴに遅れをとったニューヨークも19世紀末には、高層化競争においてシカゴから主役の座を奪うことになります。
(次回へ続く)
前回は鋼材の種類やJIS規格品、大臣認定品について紹介しました。
建築の骨組みにするためには、鋼材をメーカーで製造しファブリケーターの工場で加工します。本当ならこの工場で全ての骨組みを組み立てて現場に持っていければ良いのですが、運搬や施工の理由から現実的には不可能です。そこで、鋼構造では部材を細かく分断し、それらを繋ぎ合わせる接合部がいくつか存在します。接合部は骨組みの形態を保ち、部材から部材へ力を伝達するとても重要な役割を持っています。人間でいうと関節のようなものです。当然ながら設計や加工運搬、施工の各段階で手間を要し、また問題を生じやすい箇所であり、地震での被害も多数報告されています。裏を返せば、この接合部の加工や施工に配慮すれば、安全性はもとより工期の短縮や工費の削減に繋がるのです。
接合部の接合方法には、リベットや高力ボルトを用いた接合と、溶接による接合があります。近年は熟練した溶接工の数が減少していることが問題になっています。また、接合部は「継手」と「仕口」に大別されます。継手は同じ部材を同じ方向に接合した部分であり、H形鋼では高力ボルト、角形鋼管では溶接によって現場で接合されることが一般的です。仕口は2つ以上の部材が異なる方向や角度で接合した部分であり、鋼構造の骨組みでは柱梁接合部(柱梁仕口部)が重要な仕口です。柱梁接合部は柱と梁の交差部分であり、溶接によって工場で接合されることが一般的です。この柱梁接合部は、兵庫県南部地震で損傷や破断など多くの被害が報告され、鋼構造では最も重要な部分の一つであり、現在でも多くの研究がなされています。このような継手や仕口の破壊は、構造物に大きな損傷をもたらす可能性が高いため、部材本体が損傷しても接合部は損傷しないということが現在の耐震設計の基本となっています。
今回は鋼構造のほんの一部を紹介しました。鋼は本来強度が高く、粘り強い性質を持っており構造材料としては優れた性能を持っています。しかしながら骨組みとして使用する場合は注意すべき点も多くあります。そのような弱点を見極め適材適所で材料や加工方法を選定し、鋼の持つ長所を存分に活かすことが構造設計者の腕の見せ所といえるでしょう。
建築業界では、木造のことをW造、鉄筋コンクリート造のことをRC造、鉄骨造のことをS造と略します。
Wはwoodで木の略。RCはReinforced Concreteで補強(強化)されたコンクリートという意味です。そしてSはSteel、つまり鋼です。鉄骨造でしたら、鉄=Iron・I造になるのかと思いますが、鉄ではなくSteel・鋼構造なのです。
今回はそんな「S」の世界を少しだけ紹介します。
鉄と鋼は先ほど述べたように明確に異なります。大きな違いは含まれている炭素の割合であり、それによって分類されています。炭素の割合が0%~0.008%を鉄、0.008%~2.0%を鋼、2.0~6.67%を鋳鉄と呼びます。鋼材の特性は含有する炭素量によって大きく左右され、炭素量が増えると強度・硬度が高くなりますが、靭性が低下して脆くなり溶接性も低下します。鋼の中でも炭素量によって、極軟鋼、軟鋼、半硬鋼、硬鋼、最硬鋼に分類されています。この中で「軟鋼」が建築や造船、橋梁、ボイラーで広く用いられています。また他にも、合金鋼、高張力鋼、耐候性鋼、溶接用鋼、快削鋼、耐火鋼、低降伏点鋼など、様々な種類の鋼材が用途別に分類されています。
建築物の主要構造部に使用する材料は、大臣が定める指定建築材料でなければなりません。また、鋼材は日本産業規格(JIS)に適合した工業製品として、その性能が安定的に供給されるものでなければなりません。ここで、建築鋼材で最も多く使用される材質規格を3つ紹介します。これまで長年使用されてきたものは、一般構造用圧延鋼材(SS材,Steel Structure)と溶接構造用圧延鋼材(SM材, Steel Marine)です。SS材は広く用いられ、流通量も多く代表的な材料ですが、建築では主要部材(柱や大梁)に用いられることは基本的にありません。SM材はもともと船舶に用いるために溶接性を高めた鋼材です。建築でも重要な溶接部分に用いられることがあります。1994年に新たに建築構造用圧延鋼材(SN材,Steel New)が制定されました。SN材はさらにA種、B種、C種に細分されています。それぞれの分類内容は割愛しますが、特に建築の主要構造部ではB種が使用されます。地震国である日本では、鋼構造には十分な変形能力を確保して粘り強く抵抗できる構造とすることが、現在の耐震設計の基本とされています(構造コラム第11回参照)。また、ラーメン構造では柱と梁の接合部分で溶接が多用されており、この部分の健全性確保も最重要項目となっています。このようなことから、SN材B種では強度やリン・硫黄の成分上限値、炭素量や衝撃値などが厳密に規定されており、H形鋼の柱や大梁、片持ち梁ではSN材B種を用いることが一般的です。
JIS規格品以外にも建築鋼材として使用される材料があり、それらは大臣の認定を得る必要があります。主要部分で溶接が採用され、部材が塑性化することが想定される場合は、SN材B種に要求される性能と同等以上の性能が要求されます。中低層のラーメン構造の柱には、冷間成形角形鋼管が多く使用されています。圧延コイルをロール成形または、厚鋼板をプレス機で角形に成形し、シーム(継ぎ目)を溶接するなどして造られます。この冷間成形角形鋼管は従来STKR材(Steel Tube Kozo Rectangular)が用いられてきましたが、代替品としてロール成形角形鋼管(BCR材,Box Column Roll)とプレス成形角形鋼管(BCP材,Box Column Press)が大臣の認定を受けています。これらは材質がSN材B種やC種に準拠しており、降伏点の上下限幅も厳密に規定されています。
(次回へ続く)
構造設計では、特定の災害への対策として計算により力学的に求めた部材断面を状況に応じて大きくすることがあります。例えば、火災に対しては、木造建築物の燃えしろを確保するために、また塩害に対しては、鉄筋コンクリート造のかぶり厚を確保するためなどがあります。
木造建築物の燃えしろ設計では、耐火仕上げが行われていない現し(あらわし)の柱や梁に対して、火災により焼失する断面を想定し部材断面を大きくします。木材は表面から燃えていくため、中心部の強度はしばらくの間保たれます。そうすることで、建物が崩壊するまでに建物の使用者が避難する時間を確保するわけです。
燃えしろを考慮した木造建築物は、準耐火建築物となります。準耐火建築物で、木材を現しにしたい場合は、燃えしろ設計を行い部材を大きくすることで実現可能です。しかし、木材の現し部1面毎に3~4㎝大きくする必要があるので、通常よりかなり大きな部材断面になってしまいます。
沿岸地域に建物を建設する場合、塩害に注意する必要があります。
特にその可能性が高い地域では塩害危険地域とされており、その危険度によってランクが区分されています。鉄筋コンクリート造の場合、強風時などに海水のしぶきが飛来し、コンクリート面が海水でぬれる可能性がある地域では、かぶり厚を大きくとる必要があります。かぶり厚とは、鉄筋の表面からコンクリート面までの厚さのことです。
アルカリ性のコンクリートに酸性の海水がかかると、コンクリートが中性化してしまいます。コンクリートが中性化すると、鉄筋が錆びてしまいます。鉄筋が錆びると鉄筋の体積が増大してコンクリートがひび割れ、その隙間から海水が入りまた鉄筋が錆びるという悪循環に陥ります。このように躯体を劣化させないためにかぶり厚を大きくすることは有効です。
通常地上部で土に接していない部分での最小かぶり厚さは30~40mmに対して、塩害対策の被り厚は70mm(仕上げがある場合60mm)ですので、倍以上の寸法となります。その為、部材断面が大きくなり重量も重くなります。
構造設計では地震や台風だけではなく、火災や塩害、凍害などの対策も行っています。部材断面を大きくすることは、建設コストが上がり、建物の自重も大きくなり構造設計的に難しくなりますが、それでも災害には対策が必要なのです。
構造計算をしていると、たびたび「安全率」という言葉が出てきます。今回は、知っているようで意外と知らない安全率についてご紹介します。
安全率の考え方は建築分野に限った話ではなく、工学全般はもとより化学や航空宇宙、原発など多岐に渡って適用されます。そもそも安全率とは、「構造物や材料の極限の強さと、安全に使用できる限度の許容応力との比」(前者/後者)(出典:デジタル大辞泉(小学館))という定義です。残念ながら、私にはこれを読んでも何のことかさっぱりわかりません。
1本のロープを思い浮かべて下さい。このロープは10の力で破断(ちぎれる)するものとします。一方、実際使用するときは安全性をふまえて、最大でも1の力までしかかからないような設計とします。この場合安全率は、「10/1=10」となります。このように、安全率とはその物が本来持つ強度に対して、どれだけの余裕をみた設計にするかを数値化したものです。
建築分野では、鋼とコンクリートが材料として良く使われます。建築で使う鋼の安全率は「長期荷重:1.5、短期荷重:1.0」とします。ここでは鋼の「極限の強さ」を「降伏強度」と決めています。鋼に力を加えると変形しますが、力が加わらないと元の形に戻ります。しかし、ある一定の力を超えると、力を加えるのをやめても変形が元に戻らない点があります。このときの強度を「降伏強度」といい、この性質を鋼が「降伏した」といいます。すなわち、鋼が降伏するときの強度を1としたとき、長期荷重(建物の自重など常にかかる荷重)に対して、2/3の力までしかかからないような設計をせよということになります。つまり短期荷重(地震や風の荷重)に対しては降伏強度ぎりぎりまでの力で設計してよいということになりますね。ちなみにコンクリートは「長期荷重:3.0、短期荷重:1.5」です。ということは鋼よりコンクリートの方が、より安全性を見込んでいるということになります。
建築以外での安全率はどれくらいの数字が設定されているのでしょう。エレベーターのかごを吊るすロープは、「安全率10以上」としています。人の命に直接かかわるので、これはかなり安全性が見込まれています。一方航空宇宙では、「安全率1.15~1.25」とかなり低く設定されています。これは安全のための材料や設備などが、経済性に大きく影響してしまうからです。その代わりに、整備に多くの時間をかけ、品質管理を徹底して行います。
材料や用途などによってさまざまな安全率。もしものときに、きっとその本質が発揮されるでしょう。
前回は、シドニー オペラハウスのコンペ案について、その屋根曲面のスケッチを数学で解析することの困難さについてお話しました。設計者であるヨハン・ウッツオンの「卵の殻のようになめらかな曲面にしたい」という強い意志を実現しようと、オヴ・アラップと構造設計技術者達は、想定を超える長期間、苦心を重ねることになります。
まずは、屋根の曲線を放物線に見立てて、解析作業が始まりましたが、シェルの足元に作用する力があまりにも大きくなり過ぎて、設計出来ないことがわかりました。この強大な力に対応するため、シェルを2重構造とし、その中に鉄骨トラスを組み込む案、開口部をルーバー状の壁で補強し、重なりあう3つのシェルを一体とする案、等々も提案されました。しかし、ウッツオンは1枚の滑らかなシェルに強くこだわり受け入れませんでした。
それらの検討に、3年以上の膨大な時間と技術を投入した結果、卵の殻のようになめらかなシェルは、どうやっても実現不可能であることがわかりました。結局、屋根曲面を無骨なリブで補強する案で進めることになりました。
残念ながら、アラップと彼が率いる一流の技術者集団をもってしても、ウッツオンのスケッチに描かれた曲面の実現が、著しく困難なチャレンジであることはわかっても、実際に不可能であることを見抜くのは難しかったようです。当時はシェル構造の黎明期であり、世界各地で、次々と斬新なシェル構造が実現し、その可能性が大きく広がっている時期でした。シェル構造の未だ秘められたポテンシャルを引き出せば、もしかしたら実現可能かも知れないと思わせる絶妙な説得力が、ウッツオンのスケッチにはあったようです。
しかし、シェルのような曲面を用いた建築物では、いかに設計するのかということと同時に、いかに造るのかという施工上の諸問題が、建築の本質にも関わる重要な論点となります。
シェル構造の建設コストは、一般に構造体そのものよりも、型枠・支保工により多くの費用がかかります。小規模なものであれば、幾何学に乗らない任意形状でも手間をかければ造ることはできますし、形が似ていれば型枠等もまた別の現場で再利用が可能です。
しかし、シドニーオペラハウスのような単一のビッグプロジェクトでは、繰り返しのない複雑な曲面では、型枠の作成に膨大な時間とコストがかかりすぎ、現実的には建設不可能になってしまいます。
そこで、ウッツォンは、屋根の複雑な曲面をひとつの球形の一部と見立てるアイデアを思い付きます。全ての曲面をひとつの球の曲面から切り出す。球であれば、どこでも曲率は一定ですから、型枠はいくらでも再利用できますし、工場で効率的にプレキャストすることも可能になります。方針が決定され、ようやくプロジェクトは実現に向けて動き出すことになります。
ウッツォンはコンペを勝ち獲ったものの、これほどの巨大なプロジェクトを担当した経験もなく、事務所の体制も整っていませんでした。オペラハウスの施工は、設計が終わる前からスタートし、現場は刻一刻と進むなか、それでも実現にこぎつけられたのは、構造設計者アラップのマネージメント能力によるところが大きかったといわれています。
構造設計事務所アラップ社がオペラハウスの構造設計に費やした時間は、37万5000時間に及んだそうです。これは、「18人のエンジニアが10年間その設計に専念した」時間に相当します。しかも、携わったのは、当時、超一流のエンジニアばかりです。
シドニーオペラハウスは、当初4年で完成するはずだったものが、14年かかりました。建設も半ばの1966年には、工事の遅れの責任を取るかたちで、ウッツォンが設計者を解任されるという衝撃的な事件もありました。しかし、ウッツォンが解任されてもアラップ社は解任されませんでした。当時の関係者が、アラップ社抜きでは、工事を完成させることが出来ないと考えていた証左ではないでしょうか。
2007年には、 世界遺産に登録されたわけですが、その選考基準でも、「建築形態」、「水景上の優れた立体芸術」、「世界的に著名な偶像的建築」等の言葉と並んで、「構造設計」が挙げられており、アラップ社の貢献について言及されています。優れた技術者集団は、その持ちうる「技術一本で勝負する」と、時代の変化とともに淘汰されていくことを心得ているのです。
世界三大美港の一つ、シドニーのポート・ジャクソン湾に突き出たベネロング岬に、総合芸術劇場のオペラハウスが立っています。
屋根・外壁は連続した曲面で構成されていて、白色と淡い桃色の釉薬をかけたスウェーデン製のタイルが張られていて、その船舶の帆のような、あるいは貝殻を合わせたような独特な外観は、シドニーのみならず、オーストラリアを代表するランドマークとなっています。
2007年には、世界遺産に登録され、学術審査にあたったTICCIH(国際産業遺産保存委員会)は、「コンクリートの新しい使い方を提言し、独創的な構造を支えるため新たな補強材のリブを考案したことは将来的な建築の可能性を広め、その意匠は創造性と革新性を兼ね備えている」と評価しています。
シドニー オペラハウスの建設工事は、当初4年の工期を見込んでいましたが、完成までに14年もの年月が費やされました。それに伴い、予算においても、計画時見積もりの700万ドルから、14倍の1億ドル以上に膨れ上がりました。現代において、14年という工期は、建築というよりも、土木のダム工事等のスケールにふさわしい年月です。工期と予算の大幅な超過をうけて、工事半ばで設計者の建築家は解任されることになります。
その屋根・外壁の曲面が、いかに実現困難なものであったか。設計者であるデンマーク人建築家ヨーン・ウッツォンと、構造設計者オヴ・アラップは、どのように、その困難に立ち向かったか。ヨーン・ウッツォン解任後もプロジェクトに残留したオヴ・アラップの取り組みと、構造設計者の役割について、20世紀の建築史上最大の難工事のひとつとされている、シドニー オペラハウス完成までの紆余曲折のストーリーをご紹介していきたいと思います。
1958年、シドニー港に突き出す岬の先端にオペラハウスを建設する計画が立ちあがり、国際コンペが実施されました。世界から200件を超える応募が集まり、国際的にはまったく無名のデンマーク人建築家ヨーン・ウッツォンが選ばれました。ウッツォンはフリーハンドで外観スケッチを描き、風をはらんで重なり合うヨットの帆ような、そのなめらかで優雅な曲線は、審査員のみならず、当時の世界中の人々を魅了しました。
しかし、このスケッチは、解析することもできなければ、つくることも出来ない、言ってみれば空想上の産物でした。薄い曲面は、鉄筋コンクリートのシェルとして建築的に実現されるわけですが、この時曲面に直交する力が発生すると、リブや折板構造等による補強が必要になります。余計な補強のない、なめらかな曲面とする場合は、曲面に直交する力をほとんど負担出来ないので、曲面に沿った軸力のみで力の流れを伝達できる適切な形状を選ぶことが重要です。
「シェルの内面を卵の殻のようにスムーズにしたい」というウッツォンの意向が、構造設計者であるオヴ・アラップと彼が代表を務めるアラップ社を3年以上にわたって苦しめることになります。
まずやらなければならなかったのは、フリーハンドで描かれた曲線を数式で表現できる幾何学形状に置き換えることでした。パソコンも計算プログラムも整っていない当時、複雑な曲線を扱うには、高度な数学的理論を駆使して手計算で解かねばなりませんでした。そのために、なんとしても幾何学形状に置き換える必要がありました。
まずは、ウッツォンが描いた曲線が放物線に近いことから、放物線案をもとに検討が始まりました。形状を数式で表現出来さえすれば、計算が可能になります。しかし、事はそれほど簡単な話ではありませんでした。
(次回へつづく)
構造設計者が構造計算をするにあたり、建物にどのような力がはたらくか、その力に対して柱や梁は安全か、ということを確かめなければなりません。昔はそろばんや計算尺、電卓を使って計算していましたが、その後構造計算プログラムが登場します。構造計算プログラムにはいくつか種類があり、大きく分けると3つに分類できます。
一つ目は応力解析プログラムです。これは骨組みにどのような力が生じるかを解析するプログラムで、形状が複雑な骨組みも簡単に解析することができます。
二つ目は個別計算プログラムです。これは、応力解析プログラムで生じた力や部材にかかる荷重から、その部材が安全であるかを確認するプログラムです。この作業を断面算定といい、構造計算の中でも最も重要な項目の一つです。かつては図表などを用いて断面算定をしていましたが、個別計算プログラムが登場してからはより正確で大幅な時間短縮が実現できました。
そして三つ目は一貫計算プログラムです。建物の形状や規模、部材の材料や断面、荷重データなどを入力すると、応力解析や断面算定も含めて個々の部材や建物全体の安全性を一貫して計算するプログラムです。複雑な形状の建物では、なかなか実情通りの骨組みとして応力解析することが難しいですが、法律や告示などの規定を満足していなければメッセージを表示してくれるなどの機能もあり、大変便利なプログラムです。現在構造計算を行う際はこの一貫計算プログラムが主流となっています。
構造計算プログラムは、これまで繰り返し手計算を行っていた煩わしい計算をコンピューターが全て行い、計算スピードは格段に向上し、計算ミスも少なくなりました。さらに近年のコンピューター性能の向上に伴い、超高層ビルなど膨大なデータ量を有する計算も短時間で行えるようになりました。今や、計算プログラムは我々構造設計者にとって欠かせないものとなっています。しかし、便利な道具も使い方を間違うと、結果を大きく誤ることもあります。
とりわけ一貫計算プログラムが普及してから構造設計を始めた若手技術者にとっては、計算プログラムの中身を全て理解することは容易ではありません。したがって、「よくわからないが計算結果がOKなので問題ないだろう」という考えに陥ってしまいがちです。しかし、一貫計算プログラムを使うには技術者自身の「高度な工学的判断」が必要となるのです。
一貫計算プログラムに全て委ねてしまうのではなく、プログラムはあくまで「道具のひとつ」であることを肝に銘じておかなければなりません。
構造計算のなかで、建物にかかる地震の力を算定する際に「地域係数」という数字を使います。これは、日本全国で一般的に地震が起こりやすいとされる地域を1.0として、過去の地震被害などをふまえて0.9、0.8、0.7まで「地震の力を低減しても良い」とした数字で、国土交通省の告示で定められています。
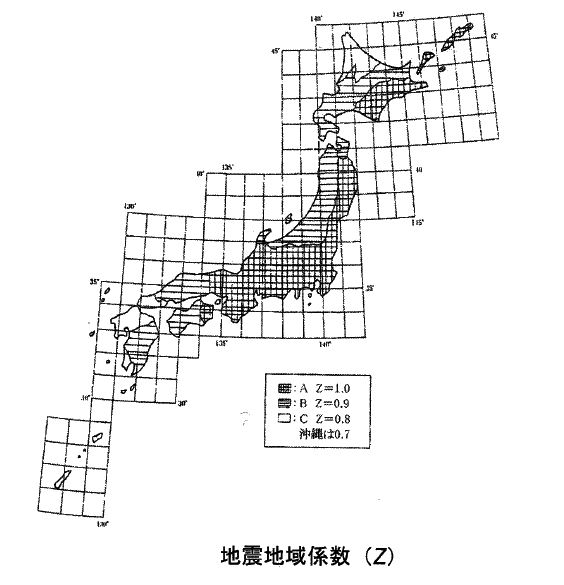
1950年(昭和25年)に建築基準法が制定されたときは、この地域係数はなく、全国同じ地震の力を想定して構造計算が行われていました。その後1952年(昭和27年)に当時の建設省が告示を制定して地域係数が定められました。この制定の基になったのが、地震学者の河角広博士のハザードマップ(河角マップ)でした。このマップは、日本の有史以来過去にどの程度の地震がどれくらいの頻度で発生し、今後も同程度の地震が発生するであろうと想定して、日本全国に細かく加速度をプロットしたものです。この河角マップから都道府県ごとに1.0から0.8までの数値が割り当てられました。
2016年4月に発生した熊本地震に関して、被害のあった地域では地域係数を0.9または0.8と定めています。つまり熊本は、全国的にみて過去の地震の被害が少なく、これからも大きな地震被害は起こりにくいであろうと想定されていました。これは、地域係数が人間の有史から想定されたものであり、人間が経験していないもっと昔のことなど考慮されていないからです。このことからも、人間が経験した範囲で定められたこの数字について、本当に必要なものなのか?と疑問が残ってしまいます。しかしながら、被害を受けた多くの建物が2階建ての木造で、これは地域係数を使った構造計算はしておらず、簡易な計算方法で建てられたものでした。ですから「地域係数を低減したから被害が大きくなったのだ。」とは必ずしも言い切れません。
沖縄県では地域係数が0.7と定められています。実は、沖縄県は本土の1.0と同じほどの地震を経験しています。もっと言うと、鹿児島県は大部分が0.8であり、奄美大島とその周辺諸島は1.0と定められています。0.8から南下して1.0となり、海を渡って0.7とはかなり不思議な値になっていますね。これは、沖縄県の地域係数が地震被害から決められたものではなく、歴史的な背景があるからです。地域係数が定められた1952年、沖縄はまだアメリカ領でした。そのため日本の法律が適用されず、1950年より前の基準法で設計されていました。そして1972年、沖縄がアメリカから返還され沖縄の地域係数を制定するとき、1.0にするとそれまで想定していた2倍の地震で計算しなければならなくなりました。それはさすがにやりすぎだろうということで0.7という数字に落ち着いたようです。
今この地域係数を、「もっと精密なものに改訂すべき」または「完全に撤廃すべき」という意見があり、議論を呼んでいます。これからも「想定外の地震」が起こることは大いに予想できますが、撤廃すれば低減によって設計された建物は「既存不適格」になってしまいます。この数字の扱いについては、設計者はこれからも付き合っていかねばならないのです。
※参考文献
大崎順彦:地震と建築、(岩波新書、1983年8月)





